4.8 Biophysics of interactions of ELF EMF with biological systems

The fundamentals of the interactions of EMF with matter were elucidated over a century ago and succinctly stated as the well-known Maxwell equations. Years of successful application of these principles for practical advances has left little doubt about our ability to understand and predict electromagnetic phenomena when the details of the system and fields are completely described. Application of these principles to biological systems, however, is very difficult because of the extreme complexity, dynamic nature, and multiple levels of organization in living organisms. In addition to their structural and biochemical complexity, biological systems are also electrically very complex and have widely ranging conductivities and dielectric properties.

The difficulties encountered in applying electromagnetic theory to the enormous number of potential interaction sites has slowed progress in understanding the possible biological and health effects of EMF. Knowledge of the mechanisms and sites of interaction could be used to identify appropriate dose metrics, to predict dose-response characteristics, to design better experiments, and to assist in determining whether harmful effects are likely at specific levels of exposure. The impetus for developing such an understanding is clear.

Several physical interaction mechanisms have been proposed to explain the possible biological effects of EMF. Most are based on the well-known electromagnetic interactions with inanimate materials that can be observed experimentally in the laboratory at sufficiently high electric or magnetic field strengths. The controversy surrounding the application of these mechanisms to explain the biological effects of environmental exposure to EMF arises for two reasons. First, the field strengths and resulting forces associated with these exposures are very small. Second, the weak signals produced by field exposure must compete with the noisy background of endogenous electric fields and normal thermal fluctuations.

An additional complication in evaluating interaction mechanisms is the complex cascade of information processing that is involved in normal cell physiology. Physical theory focuses mainly on the first step in the detection of fields: conversion of energy from the field into physical or biochemical changes. Measurable biological effects may well occur far downstream from such interactions, thereby obscuring characteristics such as dose-response that are important for identifying the physical basis of the initial interaction.

The research discussed in this section is useful for addressing four essential questions:

1. What are the mechanisms by which EMF interact with biological systems?

2. At what levels of exposure are effects due to these mechanisms plausible?

3. What experimental evidence exists in support of these mechanisms?

4. Do these mechanisms have implications for the interpretation of in-vivo and epidemiological results?

It is important that a given study clearly state which of the above questions is being addressed. Studies that address only theoretical signal-to-noise, for example, can be used to answer question 2 but not the other questions. Because of the complexity of biological structure and function, it can be argued that the presently available theoretical models are insufficient to predict or exclude the possibility of biological effects at specific levels of exposure. The rationale for this argument is that detailed knowledge of local noise environments, amplification, and specificity arising from spatial coherence of the field, dynamic processes (e.g. frequency encoding of biological signals), and other factors is not available. Only when every potential interaction site has been evaluated can the possibility of such effects be logically excluded.

Nevertheless, the reasonableness of a health concern is one of the first criteria for deciding how much attention should be given to it. The results of epidemiological studies, for example, are often evaluated in terms of Hill's criteria, one of which is the plausibility of a suggested causal relationship. Epidemiological studies form a large fraction of the basis for concern about exposure to EMF, and interpretation of their results requires a decision about whether there is a plausible underlying mechanism of interaction with EMF that could be responsible for the reported results. The current accumulated body of theoretical work provides more detailed guidance for experimentalists about the plausibility of effects than was available a few years ago. Although differences in findings persist, there is general agreement about the plausibility of effects at some levels of exposure, agreement about the lack of explanatory theoretical bases at other levels of exposure, and controversy about the explanations for effects at intermediate levels.

The need for a theoretical mechanism would be reduced if identical or similar experimental results in vitro or in vivo were available from many laboratories. The lack of such experimental support increases the role of theory in addressing questions of plausibility. Thus, purely theoretical investigations of interaction mechanisms are perhaps more relevant in evaluating the biological effects of EMF than they would be in disciplines in which robust experimental results are abundant. One problem in research on EMF is the complexity of the exposure environment, as described in section 2. Unless biologically relevant exposure parameters are identified, biologists must search a massive range of exposure parameters with few guiding principles.

Few experimental studies are available of the biological effects of EMF at the field strengths commonly associated with residential exposure (< 0.5 µT). The increased risks suggested by most epidemiological studies of EMF at these strengths are far too small to be observed in vivo. It is uncertain that the biological changes associated with the small increased risks (e.g. one additional case of childhood leukemia per 10 000 exposed children) could be observed as measurable changes in vitro.

Some attempts have been made to test the proposed mechanisms of EMF interactions experimentally. The papers that are considered in this section directly address questions 1 and 3 above. Although in-vitro results do not provide definitive evidence for human health effects, they can provide critical information on important exposure metrics and on intermediate end-points that may guide the search for health effects.

4.8.1 Biologically important interactions at the molecular level

Early attempts to explain the biological effects of EMF focused on simple application of electromagnetic theory to calculate the forces on biological molecules and the energies transferred to them by weak EMF. The extremely small magnitude of these interactions led many investigators to conclude that they would not occur at normally encountered field strengths. More recent theoretical analyses have demonstrated that spatial and temporal averaging processes (e.g. arrays of ion channels, synchronized cell populations, multiple receptors, and charged species on cell membranes) substantially reduce the predicted detection thresholds.

4.8.1.1 Forces and torques on ions and molecules

When the original ion (or electron) velocity is due to an electric field E0 (which could be endogenous), it can be expressed in terms of the electrical mobility µe> as v = µe E0. The transverse force resulting from application of a magnetic field would then be ET = (F/q) = v x B and the ratio

       Eq. 4.1

Since the mobility of ions in biological fluids (Pethig, 1979) is on the order of 10-7 m2/V s, this ratio would be < 10-11 for B < 10-4 T. The value of µe for electrons inside DNA (Arkin et al., 1996; Meade & Kayyem, 1995; Murphy et al., 1993; Stemp et al., 1995) or inside mitochondrial membranes (Nicholls, 1982) is not yet known.

When an electric field is alternating, the dipole moments p of molecules due to displacement of counter-ions are not lined up with the applied electric field (owing to finite surface conductivity and resulting time delays), and consequently a torque is produced that gives rise to continuous rotation (Fuhr et al., 1986; Pohl, 1983). The electric fields necessary to sustain this rotation, even in water (where the opposing viscosity is only h = 10-3 N s/m2), however, is several kilovolts per meter inside the fluid. This viscous torque opposing the rotation is given by Stokes' law for a sphere of radius a by

T = 8ph a3        Eq. 4.2

where  is the angular velocity. On individual protein molecules after folding, the quasi-permanent electric charge distribution is nearly symmetrical. Most protein molecules have therefore a relatively small net dipole moment, considering their large size (Takashima, 1989). Typical values of p are in the range of 500 Debye units (500 x 1.6 x 10-29 = 8 x 10-27 C m), but can be larger for very large molecules. The torque exerted on such a protein molecule by the 2.5 V/m electric field inside the membrane of a 20 µm cell, which is produced by a 10-3 V/m electric field in the fluid outside the cell, would then be 2 x 10-26 N m. By comparison, the value of the endogenous torque measured on the 'g' subunit of the mitochondrial F1 ATPase, which receives energy from ATP hydrolysis, is 4.5 x 10-20 N m (Noji et al., 1997). Relatively large torques can be exerted even by magnetic fields less than 10-4 T on particles, including some of endogenous origin, with high magnetic permeability (Adair, 1993; Frankel, 1986; Kirschvink, 1992a; Polk & Wu, 1994). This mechanism is discussed below.

4.8.1.2 Perturbation of chemical reactions

The energy of the weakest, transitory, but nevertheless biologically very important chemical bond-that due to Van der Waals' forces-is about 1 kcal/mol (corresponding, on a per particle basis, to 1.62 kBt, where kB is Boltzmann's constant and t = 310 °K) (Stryer, 1989). The energies We and Wm shown on Figure 4.2 are given per unit volume. The volume of an enzyme molecule with a molecular mass of 106 (Price & Stevens, 1989) and a density of 1.7 x 103 kg/m3 (Stryer, 1989) is 10-24 m3. Over this volume, the electric energy in a medium with relative dielectric constant er ~ 10 (as inside a cell membrane) would be about 3 x 10-34 J < 10-13 kBt for a 2.5 V/m electric field. Such a field would be produced inside the 6 nm thick cell membrane of a 20 µm diameter cell by a 10-3 V/m external field. The magnetic energy over the same volume due to a 10-4 T magnetic field in a material with the magnetic permeability of free space would be 4 x 10-27 J ~ 10-6 kBt.

The assumption that the electric field within very complex biological structures is uniform is, of course, highly unrealistic. Furthermore, the maximum potential energy pE of the electric dipole with volume v in a field E is considerably larger than the available electric energy obtained by the product Wev. The fixed charge distribution of the dipolar molecule would modify the electric field in its vicinity by inducing charges on the interface of the surrounding dielectric (Coelho, 1979), the resulting energy Wr depending very much on the shape of the molecule and the electrical characteristics of the surrounding (probably inhomogeneous and anisotropic) structure. The enzyme molecule considered here (of molecular mass 106) might have a dipole moment of 2000 Debye units (3.2 x 10-26 C m), giving a maximum value for the alignment energy pE of 8 x 10-26 J ~ 1.9 x 10-5 kBt. Thus, the potential energy due to an applied 10-3 V/m field (leading to 2.5 V/m in the membrane) can be specified only as 10-13 kBt < W < 10-5 kBt in the absence of detailed knowledge of its environment and assuming that the electric field in the membrane is uniform.

All of the general considerations and numerical examples given above strongly suggest that the small electric and magnetic fields of interest here cannot be expected to supply, by themselves, the energies necessary for chemical changes (Valberg et al., 1997). Even very small fields, however, might act as control signals to modify processes that depend on metabolically supplied energy, analogous to the extremely weak radio signals, such as those transmitted over thousands of miles, that control locally supplied energy which powers a loud-speaker or large-screen television set. The exact nature of biological signal processing systems and their susceptibility to control by time-varying EMF is thus of particular interest.

4.8.1.3 Temporal averaging and time-dependent processes

Life processes depend, of course, on the quantities of chemical substances that are processed; they also depend on reaction velocities and the periods over which those processes are completed. Many biological systems contain complex feedback loops and sequences, in which very small changes at one point can ultimately lead to very large changes further along the communication chain. Prime candidates for the investigation of sensitivity to EMF are the signal processing structures: receptors on cell surfaces and inter- and intracellular messenger processes. Probably equally important are the biological 'amplifier control elements', e.g. enzymes, particularly when they also are part of signal processing systems, as in some cell surface receptors. Unfortunately, there is incomplete knowledge about the intracellular events that transform receptor-mediated signals into cell behavioral responses (Lauffenburger & Linderman, 1993); more information is available about very early signal generation, which occurs immediately after receptor or ligand binding. These early signals are more closely associated with short time-scale responses, such as secretion and the release of certain cell products such as cyclic AMP, histamine, and antibodies than long time-scale behavior, for example cell migration and proliferation. For EMF fields, however, which may be active continuously over long periods, long-term biological signaling is likely to be even more important than short-term behavior.

Surface receptors fall into three classes (Lauffenburger & Linderman, 1993): those that act as ion channels, those that interact with G proteins to produce second-messenger molecules, and those that act as enzymes. Some experimental evidence indicates the second group (Luben, 1993) and the third group (Blank, 1992) are of particular interest for the effects of electric fields. Since the receptors of these two groups are quite different from ordinary ion channels, caution must be exercised in generalizing information about the electrical behavior of receptors obtained by analysis of ion channels.

Time scales that are susceptible to intervention from alternating signals are listed in Table 4.46 (Stryer, 1989), which shows the maximum turnover of some enzymes. "The turnover number of an enzyme is the number of substrate molecules converted into product by an enzyme molecule in a unit time when the enzyme is fully saturated with substrate". It is obvious that the turnover rates of some enzymes are well within the frequency range of interest in the present context, which is < 100 Hz.

Finally, in considering the possible nature of biological signals, it is essential to recognize that both frequency modulation and amplitude modulation or pulse code modulation may be involved. Oscillations in electrical potential (Jagadeesh et al., 1992)) and in the quantities of calcium and other ions have been observed in many biological systems (Berridge & Galione, 1988), as illustrated in Table 4.47 (Berridge, 1989; Lauffenburger & Linderman, 1993). Berridge (Berridge, 1989) suggested that some physiological processes are under frequency-dependent rather than amplitude-dependent control. After reviewing reports on this subject and applicable mathematical models (Goldbeter et al., 1990; Meyer & Stryer, 1991), Lauffenburger and Linderman (Lauffenburger & Linderman, 1993) concluded "that oscillations in receptor-generated second messenger systems may indeed be capable of regulating cell behavioral response in a frequency-dependent manner". It is also worth noting that the amplitude of the observed Ca++ oscillations is not significantly affected by ligand concentration; furthermore, the observed oscillations ('spiking') are clearly a non-linear phenomenon which requires models of non-linear processes for its analysis and for possible effects of even small fields (Eichwald & Kaiser, 1993).

4.8.2 Comparison of changes induced by EMF and competing physical processes

The general approach for determining the minimum fields theoretically capable of causing biological effects is a comparison of changes induced by the fields and by other naturally occurring energies and forces.

4.8.2.1 Comparison with the geomagnetic field

A representative value of the Earth's magnetic field over continental USA is 0.45 x 10-4T. Bennett (Bennett, 1994) stated that this value is "about 200 times that from typical distribution lines...sudden fluctuations often exceeding 100 mG [10-5 T] are correlated with unusual solar activity". The second part of the statement is incorrect, since even peak variations in very large geomagnetic storms at mid-latitudes rarely exceed 5 x 10-7 T (Garland, 1971). In addition, changes of that magnitude take several hours, so that induced electric fields are very much smaller than that produced by a power-frequency field, which varies 60 times per second over the same amplitude. The first part of the statement refers to a static field, which does not induce any electric field or current, although it can modify the effects of alternating magnetic or electric fields, as suggested by equations (a) and (c) in Figure 4.2 or by its influence on electron spin. Uniform linear motion of a body through a constant static magnetic field also does not induce an electric current, since the total magnetic flux through any closed contour does not change. Only tumbling motion, such as by somersaults, or rapid bending (changing the angle between a cross-sectional area and the direction of the magnetic field vector) would change the total induced voltage  and produce current flow.

4.8.2.2 Comparison with endogenous electric fields

It has been suggested that an induced 10-3 V/m 60 Hz electric field is unlikely to affect human biology, because naturally occurring electric fields from electroencephalographic, electrocardiographic, and other bioelectric sources are about 106 times stronger and imprecisely the same frequency range (Foster, 1992). Electric fields and current densities due to heart electrical activity ('electrocardiographic') have been calculated using an anatomical model based on magnetic resonance imaging with a volume resolution (1.974 x 1.974 x 3.0 mm) that is reasonably adequate for predicting fields at various body points (Hart & Gandhi, 1997). The results (Table 4.48) show that above 40 Hz the resulting average endogenous fields are well below 10-3 V/m, except in the vicinity of the heart. Recent measurements of the spectrum of endogenous fields confirm these results (Miller & Creim, 1997).

4.8.2.3 Comparison with thermal noise

Thermal noise, present in all physical systems, is an important factor in limiting the detection of weak signals. To the extent that the transmembrane channels of a cell are in thermal equilibrium with their environment, the mean square thermal noise  in such channels, considered as a simple resistor, would be the 'Johnson' noise given by

= 4 kBtRdf       Eq. 4.3

where R is the channel resistance and df its bandwidth for electrical signal transmission. As a first approximation,  could be considered the 'transmembrane potential', which would have to be measured far enough into the conducting fluid that surrounds the cell that its entire surface could be considered as at the same potential. If this is done, the resistance R in equation 4.3 is the mean membrane resistance of a membrane that is assumed to be homogeneous, and df becomes the bandwidth of a circuit in which the entire cell membrane is considered to be a single resistor in parallel with the membrane capacitance C. Subject to these assumptions, by which the cell membrane becomes a low-pass filter,

      Eq. 4.4

and       Eq. 4.5

Since       Eq. 4.6

where er is the relative dielectric constant of membrane ª 6 according to Takashima (Takashima, 1989) and Pethig (Pethig, 1979).

      Eq. 4.7

The values given by Pethig (Pethig, 1979) and Barnes (Barnes, 1986; Barnes, 1996) for cell membrane conductivity vary between 10-5 and 10-9 S/m, leading to the estimate

4.5 Hz £ df £ 45 kHz       Eq. 4.8

The actual bandwidth for both noise and signal depends, however, on the source resistance Rs (e.g. the resistance to current flow in the extracellular medium and cytoplasm) in series with the hypothetical RC parallel combination. With Rs Æ 0, df Æ oo and [V(f)/V(f=0)] = 1 for any f; while with Rs >> R, [V(f)/V(f=0)] = 0.53 at f = 1/(4 RC). When Rs ª R, this ratio is 0.78. A more reasonable circuit model, in view of the 'access resistance' of ion channels, is discussed further on in this section. Weaver and Astumian (1990) evaluated the thermal noise limit on the response of living cells, mainly on the basis of the assumptions leading to equation 4.5. For a spherical cell with a radius of 10 µm, they obtained  = 2.8 x 10-5 V. [Since they used er ª 2 rather than the probably more appropriate er ª 6, a better value might be 1.6 x 10-5 V, but the assumptions leading to equation 4.5 are so radical that the value of Vn can be considered only a rough estimate.] Relating the transmembrane voltage V on a spherical cell of radius r to the applied field E (Foster & Schwan, 1986),

V = 1.5 E r      Eq. 4.9

they obtain a value for the minimum detectable electric field E ª 2 V/m for the prototype cell with r = 10 µm. They then considered elongated cylindrical cells (radius r, length L) and found

      Eq. 4.10

where A, obtained from equation 4.3, including effects of signal frequency and membrane conductivity. In evaluating Vn they used 10-7 < s < 10-5 S/m and rather arbitrarily selected values of df ª 10 Hz or 100 Hz for the noise bandwidth. They then pointed out that 'if a cellular mechanism for signal averaging exists', the signal-to-noise ratio would improve by the square root of the number N of signal cycles during an exposure time T, or by  (since the signal would be added in proportion to N = fT while the incoherent noise would be added as ). With time averaging over 4.3 x 104 s = 12 h, and a Df = 10 Hz, they obtained a theoretical limit for bovine fibroblasts (L = 150 µm) of only 4 x 10-5 V/m at 100 Hz. Using a bandwidth of 10 Hz, they concluded that their estimates indicated that "concerns related to possible biological effects due to very weak environmental electric fields cannot be dismissed on the grounds of being swamped by thermal fluctuations". Applying similar thermal noise considerations to molecules in solution, they came to the important conclusion that "membrane constituents should be much better detectors of an applied (electric) field than isolated molecules in solution".

Gailey (Gailey, 1996) pointed out that current flowing through a channel must also pass through cytoplasm on one side and the glycocalyx at the cell surface. In this "access resistance of the channel" (Hille, 1992), RH enters as resistances (RA, RB) between adjacent channels in the circuit representation of multiple channels illustrated by Figure 4.1 (Gailey, 1996). Gailey (Gailey, 1996) showed that a reasonable approximation of the net resistance between the mouths of any two channels is given by twice RH as defined by Hille (Hille, 1992),

      Eq. 4.11

where a ª radius of channel mouth and s is the conductivity of cytoplasm. From Figure 4.1, it is clear that the noise voltage V1 across the first channel depends not only on its own noise voltage VG1 but also on the noise voltages in all the other resistances. Since RG1 is not directly in parallel with the other resistors, however, it cannot be assumed that the noise in the different resistors is correlated. Gailey (Gailey, 1996) evaluated a general expression for the normalized correlation or coherence, g(Vj,Vk), between the thermal noise in any two open ion channels, which depends on the total number of channels. The results of this calculation are given in Figure 4.2, which indicates that g for typical channel parameters can be as low as 0.002 when the number of channels reaches 7 x 104. The noise voltages for this result were obtained from equation 4.3 using d = 100 Hz, a value of 6.5 x 109 W for channel resistance, and 3.3 x 109 W for access resistance. If voltage from an external coherent source is applied to the combination of N ion channels, the voltages across all channels due to that source will remain coherent. This result is significant, however, only for open channels when RG is not very much larger than the access resistances RA and RB. For closed channels, i.e. when RG >> RA,B, the correlation coefficient g approaches 1, even for a large number of channels.

If a voltage from an external coherent source is applied to a cell with N1 open ion channels and N2 closed channels, the applied voltages will be coherent across all channels, while the noise voltages will be coherent only across the N2 closed channels and virtually incoherent across the N1 open channels. Individual channels open and close randomly. The closing and opening rate constants, a and b, for exponential probability functions for the sojourns in these states have been determined experimentally. The reciprocals are the mean open time (1/a) and mean closed time (1/b). The dependence of these constants on applied voltage Vm is generally non-linear; however, for small values of Vm the dependence can be characterized by slopes Ma and Mb. If ao and bo are the rate constants before the perturbing signal, one can write (Gailey, 1996)

a (Vm) = ao + Ma Vm Eq. 4.12

b (Vm) = bo + Mb Vm Eq. 4.13

Since the mean number of open channels N0 is related to the total number of channels by

      Eq. 4.14

it is possible to compute N0 as a function of the perturbing potential Vm from equations 4.12-4.14. Thermal noise voltages are practically incoherent across the open channels, as illustrated in Figure 4.2, and therefore add as , while the applied voltage adds as N0. This differential effect is not the case for closed channels. It can then be shown (Gailey, 1996) that the signal-to-noise ratio will improve by a factor of

     Eq. 4.15

where the signs of the slopes Ma and Mb are generally opposite. Also, for N0 ª 104 or larger, the denominator of equation 4.15 reduces to Mb ao. This improvement factor is shown in Figure 4.3 for a0 = bo. When the slopes Ma and Mb are equal in magnitude but have opposite signs, the improvement factor due to noise incoherence is only about 2; however, when Ma >> Mb (with gÆ0 and NÆ oo), the value of d(S/N) can approach 100.

4.8.2.4 Comparison with shot and 1/f noise

Biological processes experience not only thermal noise but also 'shot noise' and 1/f noise. Shot noise is the fluctuation of a variable, such as ion current, due to its discreteness (e.g. individual charges that make up the ion current) or 'granularity'. While the inevitable graininess of the environment (through collisions) appears through kBt, the graininess of the variable itself shows up as a separate source of noise and appears only when a system is not in thermal equilibrium with its environment and significant energy is passing into or from the system (MacDonald, 1962). Shot noise can generally be described by the Poisson probability distribution, where the standard deviation, , is proportional to the mean value of the variable (e.g. current through a membrane channel).

1/f noise is noise that, when described according its spectrum, increases with decreasing frequency as 1/f . This noise, which appears in a great variety of macroscopic and microscopic systems, was thought to arise at cell membranes by flow of ion current through an orifice (Verveen & DeFelice, 1974); however, recent analytical work and analysis of available data indicate that 1/f noise in biological membranes is not an inherent property of ion transport but is produced by random switching of channels between their different states (Bezrukov, 1996).

The voltage noise spectra of a frog node of Ranvier shown in Figure 4.4 indicate that total noise depends strongly on the value of the (quasi-static) membrane potential and that 1/f noise must be a major component of total membrane noise. Verveen and Derksen (Verveen & DeFelice, 1968) concluded that 1/f is the largest source of noise at the cell membrane below 160 Hz. Barnes (Barnes, 1986) estimated that 1/f noise and shot noise in a bandwidth of 1 Hz at 1 Hz in the frog node of Ranvier is 103 times greater than thermal noise; this would translate to a ratio of about 16.7 at 60 Hz.

Astumian et al. (Astumian et al., 1995) and Weaver et al. (Weaver et al., 1998) considered a situation in which the "noise drift across a cell membrane is equal to the square root of the number of molecules passing through the membrane plus the number absorbed", i.e. the typical Poisson process of shot noise. For membrane channels, calculation gives a time of about 1 h to reach (S/N) = 1 when the electric field E0 in the medium surrounding a cell with 100 µm radius is 0.1 V/m. The principle limitation of this analysis is the assumption that only deviations in the total quantity of accumulated substance greater than noise in that parameter can be detected. No role is assigned to recognition by any part of the complex cell signaling system of changes in the velocity of substance accumulation or regular periodic changes in that velocity.

Minimum detection limits for ensembles of voltage-gated ion channels were analyzed theoretically by Gailey (Gailey, 1996)) with a two-state model for channel gating. The stochastic gating of ion channels is a form of shot noise. Gailey compared the net change in charge transferred over some period of time due to a small perturbing membrane potential to the expected fluctuations in charge transferred due to stochastic channel activity. The model predicts that a 1 µV induced membrane potential can be detected after a few milliseconds by an ensemble of 108 ion channels. Because most cell types have fewer than this number of channels, the model suggests that single cells are unlikely to detect signals of this magnitude; however, groups of synchronized cells, such as those that occur in the central nervous system, may be able to detect such signals.

4.8.2.5 Magnitude of competing thermal effects

Weaver et al. (Weaver et al., 1997) suggested that molecular changes due to temperature variations within biological systems are larger than those expected from weak exposure to EMF. This statement was based on their evaluation of the temperature dependence of the chemical rate constants, k, given by Arrhenius' equation

      Eq. 4.16

and, apparently, the assumption that electric or magnetic fields could affect a chemical reaction (or 'molecular flow') only by changing the activation energy U.

Before discussing either the pertinent numerical results or the assumptions that were apparently made, equation 4.16 must be discussed in some detail. The energy U represents the barrier between reactants and product. In deriving equation 4.16, it is assumed that reactions proceed slowly enough that thermal equilibrium between reactants and the transition state is maintained at all times at the level of the energy barrier. Since the equation is derived from thermodynamics, it describes only the average properties of a system and not individual molecular changes. The constant A is given approximately by Wojciechowski (Wojciechowski, 1975) and Price and Dwek (Price & Dwek, 1984) as

      Eq. 4.17

where h is Planck's constant and s is a stearic factor, which can be derived from statistical mechanics and has values between 1 (atom-to-atom reaction) and 10-5 (two non-linear molecules) (Wojciechowski, 1975). At the physiological temperature t = 310 °K, the value of the ratio (kBt)/h is 6.5 x 1012/s.

The rate constant k is related to the time rate of change of product formation from reactants [C] and [D] (where the square brackets indicate concentration) by

      Eq. 4.18

where the order of the reaction is indicated by the exponents c and d. The total order of a reaction is indicated by the sum of c and d; a reaction that is of 'second order' with respect to the reactant C will obviously proceed much faster than a reaction that is of first order (c = 1). The exponents c and d are experimental quantities, which can be zero or have either integral or non-integral values. In a single-step reaction (called an 'elementary reaction'), the order of the reaction is equal to its 'molecularity', i.e. the number of molecules that must collide for the reaction to take place. When the exponents in an experimental rate law are not equal to the coefficients of the chemical balance equation (e.g. 2C === D + E), the total reaction must generally occur in a sequence of steps. If they are equal, the reaction may occur in a single step, but this is not necessarily the case (Freifelder, 1985). In complex biological systems, the order of a reaction can change during its course (Johnson et al., 1974).

It will become apparent from the discussions in the next section that electric or magnetic fields could affect both the stearic factor in equation 4.17 and the effective concentration of reactants which can interact. Thus, any calculation that shows that the effect on product formation (equation 4.18) due to a small voltage which modifies U in equation 4.16 is smaller than that caused by a temperature change Dt in equation 4.16 cannot be generalized, as Weaver et al. (Weaver et al., 1997), to assume that molecular changes due to temperature variations within biological systems are larger than those expected from weak exposure to EMF.

It should also be noted that the important chemical reactions in mammals that involve enzymes have overall rate constants that encompass the rate constants of several intermediate reactions, so that the overall reaction rate cannot necessarily be described by equation 4.16 (Price & Stevens, 1989).

4.8.3 Proposed physical mechanisms

4.8.3.1 Effects of electric fields on cell surface structures and cell attachment

(a) Polarization forces
Polarization forces have been proposed as a possible physical mechanism of the interactions between fields and cells. It has been suggested that the pronounced sensitivity of cells to low frequencies is related to the very large increase in dielectric permittivity with decreasing frequency of living tissue (Foster & Schwan, 1986). The interface of the cell with its environment is a highly charged coat, or glycocalyx, and in the presence of VLF electric fields an ion diffusion cloud develops within the glycocalyx to compensate for depletion of the co-ion species in this region (Chew, 1984). ELF excitation of this cloud is also likely to affect adjacent cells (Polk, 1992a). While the microscopic relative dielectric permittivity of the glycocalyx region remains small (< 100), the large dielectric enhancement at the macroscopic level produces a substantial force on the macroscopic collection of fixed charges on the cell surface and in the glycocalyx (McLeod et al., 1993b). The large dielectric enhancement at the macroscopic level is the large polarization per unit volume of the bulk tissue, which is due to counter-ion displacement on cell surfaces when an electric field is applied (Pethig, 1979). Thus, the gradient (-e) of the dielectric constant in the glycocalyx region is due to the cell's location within a dielectric environment created by other, adjacent cells.

The Kelvin polarization force density Fv can be derived from equation (E) on Figure 2.3. Thus, in a material with N dipoles per unit volume, each having a dipole moment p, the polarization or dipole moment per unit volume P = Np and Fv = P -E (Haus & Melcher, 1989). For non-uniform fields and non-uniform dielectrics, this can be generalized by stress tensor formalism (Stratton, 1941) to

Fv = (-1/2) E2  e      Eq. 4.19

This expression is the starting point for an explanation of at least some of the electrical forces that must be acting at the cellular level. McLeod et al. (McLeod et al., 1993b), using, apparently, the vector identity

(P . E) = (P . )E + (E .  )P + P x ( x E) + E x (  x P)        Eq. 4.20

considered only the purely electrostatic case, when  x E = 0 and  x P = 0, rather than  x E = -( B/t), and then estimated

      Eq. 4.21

where D is the thickness of the boundary layer and em its relative dielectric permittivity, while ex is the relative dielectric permittivity of the external medium; Et is the tangential electric field. The pressure, FA, at the boundary layer of area A will then be (Fv A )/A or

FA ª (ex - em) e0 Et 2 N m-2      Eq. 4.22

If one uses for ELF (Foster & Schwan, 1986) ex e0 ª 10-4 F/m and em e0 ª 10-9 F/m, one obtains FA = 10-6 N/m2 if the applied electric field is as large as 0.1 V/m. This is only slightly lower than the sound pressure at the threshold of hearing, of about 2 x 10-6 N/m2 (Beranek, 1954), which might suggest that the effect is physiologically significant at this field intensity.

Since the effect is proportional to the square of the applied field, a sinusoidally time-varying field would give a time average of E02/2, where E0 is the peak value of the sinusoidal field. Therefore, the resulting pressure would act continuously while the field is applied. McLeod et al. (McLeod et al., 1993b) suggested that this temporal integration might be responsible for the effects of low-intensity fields. They also pointed out that the pressure variation at constant frequency could excite or enhance the natural mechanical vibration frequencies of some cellular structures. Furthermore, the same small pressure applied simultaneously at the boundaries of many cells could have effects on organs or organ cultures in vitro.

Support for the importance of boundary layer pressure is provided by the findings that modulation of bone-cell function by electric fields is dependent on the density (McLeod et al., 1993a) and that the effects of fields below 100 Hz reach a peak near 30 Hz (McLeod et al., 1987c). Many of the effects seen in vitro in cells that involve neither electric nor magnetic fields are, however, also dependent on cell density.

(b) Coulombic forces
Otter et al. (Otter et al., 1998) suggested that the component of the electric field perpendicular to the cell in the glycocalyx is sufficiently large to affect cytoskeletal polymerization by the mechanism known as the Brownian ratchet (Peskin et al., 1993). The Brownian ratchet has been proposed as a means by which the cell rectifies the thermal motion of its membrane to permit it to extend cytoplasmic processes. It has also been shown that addition of a weak, homogeneous force F in combination with square-wave modulation can cause particles of slightly different size to move in opposite directions. The synergetic change in velocity caused by F can be much greater than the drift velocity that would be caused by F alone (Tarlie & Astumian, 1998).

Otter et al. (Otter et al., 1998) suggested that small imposed oscillations of the membrane add to the local thermal motion and enhance the ability of actin monomers to diffuse into the space between the actin microfilament ends and the cell membrane. Atomic force microscopy has been used to show that 1.2 nm oscillatory deflections of the cell membrane can result in 1000-nm deformations of the cell surface (20-25% of the original cell height) over 90 s when the frequency of oscillation is 15 Hz. Oscillation at lower (1.5 Hz) or higher (150 Hz) frequencies produces smaller deformations, indicating a strong frequency dependence of this rectification mechanism.

The force imposed by the atomic force microscopy cantilever in these experiments is estimated to be on the order of 0.1 pN. The surface charge density of the cell surface coat (glycocalyx) has been estimated to be between 0.001 and 0.2 C m-2 (Bongrad, 1988; Lakshminarayanaiah, 1984; Pethig, 1979). With the largest of these values, an electric field of 10-3 V/m would exert a force per unit area of rE = 10-4 N/m2. Thus, the force on the membrane of a cell 10 µm wide by 100 µm long would be roughly 0.1 pN, similar to the force shown to cause dramatic cell distortion by atomic force microscopy perturbation of the cell surface (Otter et al., 1998).

To obtain a similar pressure from polarization forces, a much larger electric field, 0.1 V/m, was required. Provided that the estimate of unbalanced charge density at the cell surface is correct, the force due to the perpendicular component of the electric field appears to have a greater effect on receptors than the combination of dielectric gradient and tangential field. It is difficult, however, to believe that electric fields much smaller than 10-4 V/m affect cells through pressure effects at the boundary layer, unless the charged protein molecules are particularly sensitive to stimuli at a particular frequency. Simultaneous, coherent pressure on many receptors and alternating pressure continued for a long time could also increase very small pressure effects above the 'noise' produced by random motion of adjacent cells.

(c) Effects of induced charge on cells
Possibly as significant as the 'push-pull' (i.e. alternating positive and negative) pressure due to the interaction of a sinusoidally time-varying electric field with the permanent surface charge on a cell is the interaction with the time-varying component, r', of that charge density, which itself depends on the applied field. r' can be expressed in terms of the component of the applied electric field, E^, that is perpendicular to the cell surface. For a long cylindrical cell of radius r, it is (Polk, 1990; Polk, 1992c).

      Eq. 4.23

At frequencies (w/2p) well below the relaxation frequency fr, the term jw/ fr is negligible. If e is the elementary charge 1.6 x 10-19 C, n0 = 2 x 1017/m2 as before, r = 10-5 m, and kBt = 4.28 x 10-21 J at 37 °C, one obtains r' = 1.2 x 10-5 E^ C/m2. If E^ = E0 cos wt, the pressure r' E^ will be proportional to E02 cos2wt, and its unidirectional time average will be F'A = 6 x 10-6 E02 N/m2. For E0 =10-4 V/m, one obtains F'A = 6 x 10-13 N/m2.

(d) Induced surface charge on cell matrix or substrate
In addition to inducing charge at the cell surface, an electric field within a tissue induces a surface charge on the extracellular matrix or other growth substrate. This induced charge can have a robust effect on processes such as protein absorption and cell adhesion, as cell matrices and substrates typically have a low fixed charge density. Recent work has shown that induced charge densities on growth substrates on the order of 0.1-1.0 µC/m2 can significantly affect cell growth and morphology through this induced surface charge mechanism (McLeod, 1998).

4.8.3.2 Cyclotron resonance and ion parametric resonance

As a consequence of Lorentz' force F = q(v x B), equation (a) on Figure 4.2, a charge q of mass m which moves at velocity v in a constant (static) magnetic flux density Bs will follow, in a vacuum, a circular path of radius Rc

      Eq. 4.24

The angular velocity wc and cyclotron frequency fc will be given by

      Eq. 4.25

If an electric field is applied as in a cyclotron (Sears et al., 1976) or induced by an alternating magnetic field, B = B0 cos wct, that has the same direction as Bs, the tangential velocity v of the charge will increase, as will correspondingly its orbital radius Rc. It has been noted that the cyclotron frequencies, fc = wc/2p, of many physiologically important ions fall below 100 Hz in the geomagnetic field ( ª 50 µT depending on latitude). For example, fc = 38.4 Hz for the 40Ca++ ion at 50 µT. Chiabrera et al. (Chiabrera et al., 1985) and Liboff et al. (Liboff, 1985) therefore proposed various mechanisms which require cyclotron motion of ions along circular or helical paths, either in transmembrane channels or at receptors on the cell surface. It has been pointed out (Durney et al., 1988; Halle, 1988; Sandweiss, 1990), however, that such motion is impossible in the dense, collision-dominated fluids of biological materials. Furthermore, ions in biological fluids are normally hydrated, and the frequency given by equation 4.25 would depend on the number of water molecules (and their total mass) in the hydration sheath of each ion (Koryta, 1982).

Despite the apparent implausibility of cyclotron resonance as a mechanism for interactions between magnetic fields and biological systems, many experiments have shown a response to combinations of static and alternating magnetic fields, which reaches, in different systems, either a maximum or minimum at the frequency fc given by equation 4.25 for various physiologically important ions. Some attempts to replicate the results independently in different laboratories have failed while others have been successful (Table 4.5).

(a) Lednev model
A refinement of the cyclotron resonance model is provided by a theory proposed by Lednev (Lednev, 1991; Lednev, 1993; Lednev, 1994), which pertains to effects that would affect transport through ion channels only indirectly. It is based on the idea that an ion weakly bound within a protein, notably Ca++ within calmodulin, can be modeled as a charged oscillator. The oscillations are metabolically excited and are at infrared frequencies. An ambient, steady (DC) magnetic field, BS, such as that of the Earth, would cause Zeeman splitting (Haken & Wolf, 1984) of each vibrational level into two levels, wA and wB, separated by the ion cyclotron frequency. Thus, wc = wA - wB. When an alternating field, B1, is then applied in parallel with BS, the resulting frequency modulation of levels wA and wB will change the probability of ion transition, P, from an excited level to some ground state of frequency w0. Applying earlier work (Podgoretskii & Khrustalev, 1963), Lednev then predicted that the time average of P will be

      Eq. 4.26

where K1 and K2 depend on the amplitudes of infrared radiation corresponding to transitions from wA and wB to w0, d is the difference in phase of the radiation from two sublevels, and the argument of the Bessel function Jn(x) is

      Eq. 4.27

The Bessel function Jn(x) in equation 4.26 leads to maxima and minima when the frequency of the applied sinusoidal magnetic field is

      Eq. 4.28

where n is an integer. Lednev's model thus not only predicts 'resonances' at the cyclotron frequency and its subharmonics but also prescribes the relative amplitudes of B1 and BS for which the 'resonance' effects should be maximized. These are given by the values of the argument x that corresponds to extreme values of Jn(x). For example, J1(x) has its first maximum at x = 1.84. The model furthermore predicts, at a fixed BS and resonance frequency fc, a variation of system response as the amplitude of B1 is varied, changing the magnitude of Jn(x).

One apparent advantage of this particular theoretical model was that it could be tested by applying appropriate fields BS and B1 to proteins in chemical reactions without the presence of complicated cells or tissue. Experiments to study the effect of parallel directed BS and B1 fields on the phosphorylation of myosin in the presence of calmodulin and troponin-performed, however, over only a very narrow frequency range-seemed at first to confirm the theoretical predictions (Shuvalova et al., 1991). A similar experiment also showed that phosphorylation of myosin can respond to purely static magnetic fields between 0 and 200 µT in the absence of an alternating field (Markov et al., 1993). An investigation of calcium binding to metallochromic dyes involving an indirect measurement of Ca++ binding to calmodulin in the presence of combined AC (50 and 120 Hz) and DC (0 to 299 µT) magnetic fields, however, failed to show any effect of the magnetic field (Bruckner-Lea et al., 1992).

The principal difficulty of the theory is that the width of the infrared spectral lines, due to vibration of Ca++ in the calmodulin molecule, must be extremely narrow (< fc) if splitting into two frequencies, separated by fc, is to be significant. Lednev suggested that shielding of the Ca++ ion within the structure of the calmodulin molecule would prevent at least Doppler broadening. Furthermore, an ion inside a molecule is largely protected from collision with atoms or molecules in the external environment.

Calmodulin is ubiquitous in living organisms and is essential to normal cell function (Cheung, 1982). It interacts with many Ca++-dependent enzymes and regulates their activity (Stryer, 1989). Since the location of Ca++ ions at four possible binding sites within calmodulin and the strength of binding at each site (Rainteau et al., 1989) profoundly influence the interaction of calmodulin with various enzymes, any effect of magnetic fields on Ca++ binding with calmodulin would affect a wide range of physiological processes.

(b) Ion parametric resonance
Blackman et al. (Blackman et al., 1994; Blackman et al., 1995) subjected PC-12 cells stimulated by nerve growth factor to combinations of AC/DC magnetic fields and found that the number of cultured cells with neurite outgrowths decreased in comparison with unexposed cells as a function of AC/DC amplitude. That behavior was, however, restricted to narrow frequency bands determined by the amplitude of the applied DC magnetic field, suggesting a 'resonance' behavior. They were able to fit their data to a Bessel function by assuming a dependence

      Eq. 4.29

in which the factor of (2) in the argument of the Bessel function accounts for a dependence on the B1/B0 ratio that differs substantially from that predicted by Lednev's equations 4.26 and 4.27. Using fairly elaborate curve fitting, they suggested that the data for PC-12 cells indicate 'resonances' corresponding to ions of vanadium, magnesium, manganese, and hydrogen. The original experiments were later replicated under double-blind conditions in the same laboratory [Blackman, In Press #1788]. Blackman et al. (Blackman et al., 1996) also demonstrated that their experimental results are not related to the amplitude of the magnetically induced electric field (Blackman et al., 1993a) and that mutually perpendicular, rather than parallel oriented, AC and DC magnetic fields evoke different biological responses.

The results obtained by Blackman et al. (Blackman et al., 1994; Blackman et al., 1995; Blackman et al., 1998; Trillo et al., 1996) for neurite outgrowth of PC-12 cells appear to confirm the Blanchard and Blackman (Blanchard & Blackman, 1994; Blanchard et al., 1995) version of the ion parametric resonance theory (equation 4.29). The results of experiments with living land snails (Prato et al., 1996), however, agree better with Lednev's original proposal (equations 4.26-4.28).

Despite these experimental results, questions remain about the validity of the ion parametric resonance theory. Adair (Adair, 1992) pointed out that it requires the radiating ion to be shielded from collision-like interactions with the surrounding material. Even if the de-excitation time of the above-ground state oscillation were as long as 0.1 s, the width of that state would be only 10 Hz, and a 16 Hz cyclotron resonance would be ill defined. Furthermore, presumably any substantial transient change in the ion-excited state would interrupt the mechanism, which depends on a specific energy difference between the split states (at frequencies wA and wB). Adair (Adair, 1992) suggested that large transient electric fields from far-off collisions would destroy the fine tuning required by the mechanism; however, such transients would most likely shift the vibrational sublevels at frequencies wA and wB equally, so that the important difference wC would be preserved. He pointed out that an ion as heavy as Ca++ would not radiate strongly and noted that the mechanism also requires perfect three-dimensional symmetry of the vibration before the perturbing alternating field is applied, e.g. equal 'spring constants' in different directions. In addition, a large set of ions would have to be excited and modulated coherently by the external field for a noticeable effect to occur.

Lednev (Lednev, 1994) responded that the model applies primarily to the effects of external fields on vibration of Ca++ or Mg++ in calcium-binding proteins and that the atomic structure of Ca++ binding sites is known from X-ray diffraction studies in a number of calcium-binding proteins, including calmodulin (Babu et al., 1988). These results indicate that the symmetry condition is satisfied. As an example, Lednev referred to the radial distribution of protein oxygens around the Ca++ at two calcium-binding sites in parvalbumin, which show sharp peaks at the identical ultraviolet wavelength (Ahlstrom et al., 1987).

Concerning the requirement that the excited vibrational mode have a 'long' lifetime (i.e. long de-excitation time) in order for the ELF field (periods, 10-50 ms) to be effective, Lednev cited Ritov (Ritov, 1976), Martin et al. (Martin et al., 1985), and Cox (Cox, 1988) to confirm that the lifetime of Ca++ and Mg++ chelated in the calmodulin-kinase complex is about 1 s.

In a detailed analysis of the ion parametric resonance mechanism, applying quantum mechanics, Engstrom (Engstrom, 1996) concluded that the model makes many predictions for biological systems that are sensitive to differences in excited states of biochemicals, and that these predictions can be tested experimentally. Another interesting direction of research is investigation of the effects of fields at angles other than parallel and perpendicular orientations. In the context of a search for mechanisms that can explain the biological effects of weak magnetic fields, a particularly important feature of the ion parametric resonance model is that it assumes no energy input from the applied magnetic field into the affected biological system. It postulates only that the energy already in the system will be redistributed. Lednev (Lednev, 1994) suggested that, for this reason, it is not applicable to a system in equilibrium such as the solution containing calmodulin and CaCl2 that was used in the experiments of Bruckner-Lea et al. (Bruckner-Lea et al., 1992) mentioned earlier in this section.

4.8.3.3 Biological electron transfer

Long-range intermolecular and intramolecular electron transfer plays an important role in conferring the specificity and directionality of numerous biological processes (Gray & Winkler, 1996). These include the classical enzyme reactions that have been suggested as a medium for field interactions (Grundler et al., 1992). Specific examples may be cytochrome C oxidation by the enzyme cytochrome oxidase and effects of EMF on Na/K ATPase function (Blank, 1992; Blank & Soo, 1992a; Blank et al., 1995). It has also been shown that a non-equilibrium chemical reaction catalyzed by a membrane enzyme can act as an active element in an external electric circuit and provide the energy for driving electrical oscillations (Derenyi & Astumian, 1998).

One difficulty in accepting biological electron transfer as a likely initial site for detection of weak externally applied electric or magnetic fields is that the endogenous energies involved in electron binding are many orders of magnitude larger than those contained in the weak fields of interest here. Electron affinity values for organic molecules generally fall within the range 0.5-2.0 eV (19-75 kBt) (Pethig, 1979). Free or diffusing electrons might, however, be affected by even weak electric or magnetic fields. As mentioned earlier, the electric mobility µe of ions in biological fluids is of the order of 10-7 m2/V s. The interaction of a magnetic field with any charged particle by Lorentz' force depends on the velocity of that particle [equation (a) on Figure 4.3]. Since that velocity v is related to the electric mobility by v = µe E0, the magnitude of effects on charged particle motion by a magnetic field B can be estimated by considering the ratio of the transverse electric field ET (transverse force/charge q) to the electric field E0 (probably of endogenous origin) that was responsible for the original linear motion at velocity v. That ratio is µeB. While the mobility of electrons over long distances along protein strands is probably also small, it could be sufficiently large in some locations for electron motion to be affected by a relatively weak magnetic field.

It has been shown that electron mobility along the p bonds in the central core of DNA strands can be surprisingly large (Arkin et al., 1996; Meade & Kayyem, 1995; Murphy et al., 1993; Stemp et al., 1995); however, it is not known whether it is large enough to make transverse deflection of electron currents due to applied magnetic fields plausible. Direct effects on DNA of externally applied EMF have been suggested (Blank & Goodman, 1997).

Another important site for consideration of possible effects on electron transfer by applied magnetic fields is the mitochondrial membrane (Nicholls, 1982), where proton and electron transfer are involved in energy conversion mediated by ATPases (Polk, 1997).

4.8.3.4 Effects on biogenic magnetite

Magnetite biomineralization occurs in the human brain (Kirschvink et al., 1992), and one line of human leukemic leukocytes was nearly 100 times more magnetic than brain tissues, giving cellular magnetic moments of ~ 10-12 A m2 (Kirschvink & Kobayashi-Kirschvink, 1993). Kirschvink (Kirschvink, 1992a) suggested that the interaction energy of even weak ELF magnetic fields with magnetic particles of magnetic domain size would be larger than the thermal energy of (1/2) kBt per degree of freedom within a system in thermal equilibrium. Using a model of magnetic particles floating in a fluid medium, Adair (Adair, 1993) proposed that a 60 Hz magnetic field weaker than 5 µT could not generate significant biological effects in the cell by acting on magnetic elements. That conclusion appears to be premature, however, because not enough is known about the relationship of the magnetite particles to other components of the cell interior or of the cell membrane to formulate a mathematical model that is adequate for precise numerical predictions.

A description of the dynamics of any kind of anchoring of the 'magnetosomes' to the cell structure would require a non-linear differential equation; even a linearized equation would have no constant coefficients unless the applied alternating magnetic field is exactly perpendicular to the geomagnetic field and the magnetosome deflection is very small. In addition, the effective viscosity of the fluid within the cell in the vicinity of the magnetosomes, which is a critical parameter in the Adair model, cannot be well specified. Even if this clearly oversimplified model is used but combined action by multiple magnetosomes within the cell is allowed, a signal-to-noise ratio well above 1 might be possible with a 60 Hz magnetic field of 2 µT (Polk, 1994). Neither estimate can be considered adequate at the present time; however, it is likely that any effect of multiple magnetosomes within a cell would make use of their coherent motion, and thus there would be no significant thermal noise limitation if the energy supplied by an applied field to a single magnetosome were much smaller than kBt. For single domain particles of Fe304, the magnetic moment is given by (Frankel, 1986):

µ = volume x 4.8 x 105 A m2         Eq. 4.30

and the energy supplying torque to a spherical particle of 60-nm diameter in a 2 µT field would already be 0.1 kBt at 37 °C. Therefore, it is important to perform further experimental work on the behavior of such particles within cells or of similar particles that might be present in cell culture media (Dobson & Grassi, 1996; Kobayashi et al., 1995). Vaughan and Weaver (Vaughan & Weaver, 1996; Vaughan & Weaver, 1998) suggested that endogenous or contaminating magnetic particles could create pores in cell membranes when magnetic field pulses are applied; however, they indicated that for simple biologically synthesized magnetosomes (radius = 10-7 m; magnetic moment = 2 x 10-17 A m2) and typical cell membranes, the estimated pulse magnitude must exceed B0 ª 1-7 x 10-2 T, and the optimal pulse duration is in the range 10-5 s < tpulse < 10-1 s. For larger contaminating particles with larger net magnetic moments, the pulse magnitudes could only be somewhat smaller, and the optimal durations are about the same.

4.8.3.5 Magnetochemistry: Effects of magnetic fields on free-radical reactions

Free radicals are important in many biological processes (Freifelder, 1985). For example, they are formed as intermediate products when light is incident upon the visual pigment rhodopsin. It has been known for some time that chemical reactions that involve free radicals are strongly influenced by static magnetic fields (Blankenship et al., 1977; Hoff et al., 1977; Werner et al., 1978), but more recent work (Cozens & Scaiano, 1993; Hamilton et al., 1988; McLauchlan, 1989) suggested that DC fields as low as 1-10 Gauss may affect such chemical processes. By implication, as is shown below, alternating fields of the same order of magnitude, acting in concert with steady fields should also affect reaction yields. The effects of even smaller alternating fields have been predicted by analytical work (Adair, 1997; Brocklehurst & McLauchlan, 1996; Canfield et al., 1994) and are discussed further on.

Observations in this area are based on Pauli's exclusion principle, which states that the electronic states of an atom can only be occupied in such a way that no two electrons have exactly the same set of quantum numbers. Thus, if there are, for example, two valence electrons in the same orbital, characterized by the same set of orbital quantum numbers, their individual spin quantum numbers must be +1/2 and -1/2; i.e. their spins must be in opposite directions. If two electrons in a chemical bond are paired in this manner and if this bond is broken, for example by incident light, resulting in two free radicals, subsequent recombination is possible only if the two electrons preserve this oppositely directed spin. Interaction with the local magnetic field-due to nuclear magnetic moments or other nearby spinning and orbiting electrons-can, depending on the particular molecular structure, either favor or destroy opposite spins. In the latter case, of now equally orientated spins, recombination of the radicals becomes impossible. Conversely, if the radical pair was formed from excited atomic states with the unpaired electrons coming from different atomic shells, they may already have equal spin, preventing chemical combination of intermediate products.

As long as the electrons have opposite spin, the products have a 'singlet' character, i.e. the total quantum number J, which characterizes the electron states, is equal to the orbital quantum number L, since the spin quantum number S = (1/2) - (1/2) = 0 and J = S + L. As the products diffuse, however, some fraction will acquire a 'triplet' character; i.e. the electron spins may become parallel, and S = ± (1/2 + 1/2) = 1 and J can have three values, L + 1, L - 1, and L, in view of the quantum rules for combination of angular momenta. If the products were initially in the triplet state, diffusion will have the opposite effect, i.e. partial conversion from a triplet to a singlet character.

The singlet and triplet states have, in general, different energies, as indicated at B = 0 on Figure 4.5. Any magnetic field, including that of nearby magnetic nuclei, will cause triplet states T + 1 and T - 1, which have electron spin in the direction of the field, to gain or lose energy. Therefore, the energy levels of these states will separate with increasing B, as indicated on Figure 4.5. Interconversion between the singlet and triplet states can occur either by external energy input or between T0 and S through a distance-dependent 'electron exchange interaction' at any level of B. At some critical level of B = Bc, interconversion between T - 1 and S is also possible without external energy input. It has been shown experimentally that this level is approximately 1 mT in a pyrene-dimethylaniline system (Hamilton et al., 1988).

Since interconversion between singlet and triplet states in the direction of greater singlet product will make chemical combination possible, application of the correct value of Bc will obviously affect the rate of chemical reaction. It is also possible that an ambient flux density (from external and internal sources) may have a value B1, which is either slightly larger or smaller than the required Bc. In that case, addition of an alternating field BA cos wt will periodically establish optimum conditions for conversion (the period 2p/w of ELF fields is much longer than the nanoseconds required for the T - 1 -> S transition). It appears therefore to be at least possible that small AC magnetic fields in the presence of the geomagnetic field could affect chemical reactions in biological systems that involve free radicals as intermediate products. Many authors, e.g. Walleczek (Walleczek, 1995), have pointed out that the spin of valence electrons in free radicals is not coupled strongly to the thermal environment and is therefore not subject to a kBt thermal noise limit.

With regard to the basic free-radical effect of magnetic fields, the frequency of an ELF field would not be recognized, since the diffusion time of the free radical is much shorter than the period of an applied ELF field. The latter would therefore be indistinguishable from a static field. It has been shown (Eichwald & Walleczek, 1997), however, that sensitivity to ELF fields results if the radical pair process is integrated into a scheme involving dynamic signaling.

Time-dependent perturbation theory with iterative solution of Schroedinger's equation has been applied to the problem of singlet-to-triplet yields in radical-pair reactions subjected to oscillating magnetic fields (Canfield et al., 1994). Considering frequencies of the alternating magnetic field between 0.5 and 3.0 MHz, which include the precession frequency of an electron (1.4 MHz) in the Earth's magnetic field (50 µT), they showed effects on triplet yield at a surprisingly low amplitude of 0.7 µT when the static field was 50 µT. They emphasized that the radical-pair mechanism is inherently non-linear and that the effects on the singlet-to-triplet yields did not always increase as the oscillating field strength was increased. Thus, if this mechanism does indeed account for some of the biological effects of magnetic fields, simple dose-response should not be expected. They also pointed out that the singlet-to-triplet yield versus frequency spectrum could be altered dramatically by simply changing the orientation of the oscillating field and that the effects of two simultaneously applied oscillating fields are not simply additive but interact in a nonlinear fashion. They concluded that such nonlinear interactions (due to second-order and higher perturbation expansion terms) of experimentally applied fields, which become more apparent at higher oscillating field strengths, with uncontrolled environmental fields may account for some of the conflicts in the literature on the biological effects of magnetic fields.

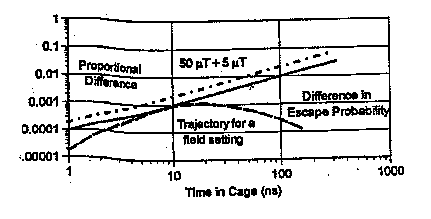
In another theoretical treatment of radical-pair re-formation by very weak magnetic fields, thus far reported only in an abstract (Adair, 1997), the author reported that, using exact calculations on an appropriately general model system, small but significant modifications of the recombination rate by a 50 µT field could be expected only under a narrow range of circumstances. The radical-pair containment time must be exceptionally long, 50 ns or longer; the hyperfine field of neither radical must be appreciably greater than that which generates a precession period greater than the cage containment time; and the characteristic recombination time of the radical pair in the singlet state must be about equal to the containment time. Fields as small as 5 µT produced no significant change in the recombination rate. He concluded that environmental magnetic fields much weaker than the Earth's field have no significant biological effect by modifying the recombination probabilities of radical pairs. The figure included in the abstract, however, shows an approximately two-to-one change of the difference in the escape probability of the radical when a 5 µT field was added to a 50 µT (ª geomagnetic) field, see Figure 4.6. For a 'cage' confinement of the radical lasting 100 ns, this is a change from 0.01 to 0.02. One might question whether such a small change in escape probability could ultimately have a large effect under some circumstances. One possibility might be the existence of magnetic field-dependent radical-pair chain reactions. Analysis of such reactions (Grissom, 1995) indicated that even a small field-induced change in the concentration of radical propagators would have a large effect on the reaction rate of the process, because each radical can cause multiple chain events. A numerical simulation (Eichwald & Walleczek, 1996b) showed that an amplification factor can be derived in some enzyme reactions from the specific relationships between rate constants. As a consequence, although the magnetic field-induced change in radical-pair recombination probability is very small, the effect on the enzyme reaction rate is much larger, for example by a factor of 1-100.

The effects of magnetic fields on radical-pair chemical reactions are firmly established, both theoretically and experimentally. Some experiments have shown that effects can occur at applied static field levels as low as 100 µT (Batova et al., 1993; Nossol et al., 1993). The effects of low-intensity ELF fields on free-radical reactions in biological systems have been studied experimentally in very few systems (Harkins & Grissom, 1994). Since studies in this area may explain many presently poorly understood experimental results (Sciano et al., 1994), it deserves substantial effort in the future.

4.8.3.6 Non-linear dynamics and application of stochastic resonance

It has been recognized for about 30 years that non-linear, non-equilibrium phenomena play a very important role in biological systems (Adey, 1975; Adey, 1981; Adey, 1983; Frohlich, 1968). Such systems are characterized by sensitivity to initial conditions, such that slight changes in one or more parameters can significantly alter the state of the system after some time. Some non-linear, non-equilibrium processes were considered in preceding sections (e.g. magnetochemistry).

The effects of electric fields on chemical oscillations have been established experimentally (Barnes, 1996; Eichwald & Kaiser, 1993; Eichwald & Kaiser, 1995; Eichwald & Walleczek, 1996a; Eichwald & Walleczek, 1996b; Kaiser, 1994; Sevcikova et al., 1992; Wachtel, 1979). Such studies have shown that biological and functional status is of fundamental importance for an effective interaction. For example, in studies of the regulation of calcium uptake by cells of the immune system, particularly T lymphocytes, either stimulatory, inhibitory, or no effects are observed for identical field parameters, depending on the degree of cellular activation. Eichwald and Walleczek (Eichwald & Walleczek, 1996a) presented a theoretical approach to account qualitatively for effects of exposure to EMF that depend on the degree of cellular activation and that show a biphasic response (stimulation and inhibition). In this model, biochemical stimulation of the cell resulted in activation of specific signaling pathways that regulate calcium dynamics in the cell (release from intracellular stores and capacitative entry). They assumed that a specific EMF-sensitive enzyme system which is controlled by these pathways becomes activated. The activated enzyme, in turn, would exert feedback control on the signal processes, thus leading to modulation of calcium entry which may affect other cellular processes that are calcium-dependent such as DNA synthesis.

One phenomenon, that is characteristic of some non-linear systems is the possible occurrence of stochastic resonance (McNamara & Wiesenfeld, 1989; Moss & Wiesenfeld, 1995), in which the output signal-to-noise ratio improves, at first with increasing input noise before it decreases as the noise increases further. The importance of this phenomenon for the detection of weak biological signals has been suggested by several authors (Grundler et al., 1992; Kaiser, 1994) and is confirmed by some experimental results (Collins et al., 1996; Douglass et al., 1993; Gluckman et al., 1996). Most applications of this theory have been based on threshold triggered systems in which a weak, below-threshold signal is raised above the threshold by the presence of noise (Moss & Wiesenfeld, 1995; Wiesenfeld et al., 1994). A mathematical model developed by Bezrukov and Vodyanoy (Bezrukov, 1996; Bezrukov & Vodyanoy, 1997b) shows that stochastic resonance can also occur in 'threshold-free systems', i.e. systems that can respond to signals of arbitrarily small amplitude. They considered time-dependent Poisson processes, such as the opening and closing of voltage-dependent ion channels, where the system output can be described as a random train of identical pulses with the probability of pulse generation exponentially dependent on the input signal. In particular, they assume that the pulse generation rate is given by

r[V(t)] = r(0) exp[V(t)]       Eq. 4.31

where r(0) is the equilibrium rate of pulse generation and V(t) is a dimensionless voltage. After publication of the paper by Bezrukov and Vodyanoy (Bezrukov & Vodyanoy, 1997b), Astumian et al. (Astumian et al., 1997) described computations made with the model that showed that the mechanism could not explain the reported finding that fields of < 0.1 V/m caused effects on cells. In their response, Bezrukov and Vodyanoy (Bezrukov & Vodyanoy, 1997a) stated that selection of more realistic cell parameters and particularly long biological integration times would give effects at lower strengths.

Galvanovskis and Sandblom (Galvanoskis & Sandblom, 1997) considered the effect of a weak sinusoidal signal on opening and closing rates of ion channels and consequent modulation of ion currents. They applied the original theory of McNamara and Wiesenfeld (McNamara & Wiesenfeld, 1989) but extended it from a single device to N ion channels subjected simultaneously to the same sinusoidal signal. A very interesting result was obtained when the underlying transition rate was assumed to be asymmetrical with the channel open time, at 10 times the closed time (but still in the order of microseconds). In that case the 'output' (i.e. the periodic component of the ion current across the membrane) contained not only the applied frequency but also several harmonics (Figure 4 in their paper). For N = 1000, a signal frequency of 50 Hz, and a 'cylindrical' human of only 10 cm in radius, the authors concluded that, under optimum conditions, even very weak low-frequency electromagnetic signals (< 100 Hz and 100 µT) could be detected in a cellular system with a large number of ion channels. They also noted that the capacity of a cell to detect periodic changes in ionic influx is essential for the effect of an external sinusoidal signal to be biologically important,. The cytosolic Ca++ oscillator, a complex system of biochemical reactions that allows a cell to create sophisticated spatiotemporal patterns of Ca++ intracellular concentrations, may function as a detector of the small component of Ca influx.

4.8.4 Summary

Examination of the forces and energies involved in biochemical processes indicates that they are far stronger than those corresponding to power-frequency electric fields inside cultured tissues or cells (< 10-3 V/m) or, equivalently, induced in humans by 60 Hz magnetic fields (< 3 x 10-5 T). Biological tissues and cells are, however, extremely inhomogeneous, and when the average electric field is < 10-3 V/m the actual field at selected locations (e.g. cell membranes) may be orders of magnitude larger. Since the magnetic permeability of tissue is usually very close to that of free space, no enhancement of the internal over the external magnetic field is to be expected, except for biogenic magnetite.

Living systems contain many structures that can sum inputs over both time and space. Thus, several thousand receptors of a particular type on a single cell may send the same message to the cell interior, where they may be added; likewise, repetitions of the same message sent over a finite period may be cumulative. In contrast, the 'noise' or random fluctuations may differ at different receptors and partially cancel. The averaging of noise over time or number of receptors can substantially improve a system's ability to detect small signals.

Most life processes, although in steady state, are far from thermal equilibrium and depend on continuous energy input. Therefore, analyses based on equilibrium thermodynamics can lead to erroneous results. Furthermore, while the 'quantity of molecular change' is certainly important, the rate at which change is accomplished is equally important: life as we know it would be impossible without the acceleration of biochemical reactions accomplished by the presence of enzymes. Furthermore, biological signal processing may not depend only-and possibly in some cases not at all-on the amplitude of a signal but also on the rate at which it is repeated (e.g. the frequency and duration of Ca++ oscillations).

Many biochemical and biomechanical processes (e.g. Ca++ oscillations and the motion of magnetizable particles attached to tissue) can be accurately described only by nonlinear differential equations. The solutions of such equations are subject to very small changes in boundary conditions and also give rise to the phenomenon of 'stochastic resonance', i.e. enhancement of the output signal-to-noise ratio by the presence (up to a certain level) of noise rather than its absence. The application of non-linear dynamics to biology is still in its infancy.

The stochastic nature and ultimate discreteness ('graininess') of electrochemical life processes is likely to enhance rather than obviate the sensing of weak electric and magnetic fields. It has been suggested that time-varying pericellular electric fields of 10-4 to 10-3 V/m can affect biological signals and that the electrical in homogeneity of living tissue can raise field intensities to this level at some points, although the field averages, calculated over a large volume, may be much lower. At 60 Hz, a 3 µT magnetic field can generate a 10-4 V/m electric field in the human body. While ion channels cannot be excluded as locations for initial detection of fields at this level, receptors and enzymes are possibly more likely sites.

The necessary non-linearity in the mathematical description of biochemical processes at the molecular level leads to time and amplitude 'windows' and guarantees that 'more' (i.e. a larger signal) is not necessarily 'better', or (depending on the point of view) 'worse'. Direct effects of time-varying magnetic fields, e.g. effects that do not occur primarily as a consequence of magnetically induced electric fields, are very likely at amplitudes above 100 µT, and there is experimental evidence to support these predictions, but their existence at lower intensities cannot be excluded. The spatial and temporal coherence of externally applied EMF and their application for extended times must play an important role in the biological detection of low-intensity fields. The entire area of biological signal transmission by frequency and/or pulse code modulation needs much further research.

All of the theories of the biological effects of small-amplitude EMF-both those that deny the possibility and those that address experimental observations-are speculative and unproved. They suffer from a lack of detailed, quantitative knowledge about the processes to be modeled, such as the 'second messenger' signal cascade, the modus operandi of many receptors, the precise origin of Ca++ oscillations and their biological function, the timing of the making and breaking of chemical bonds, chemical transition states, the dependence of magnetic fields on specific free-radical processes, and even the effective viscosity inside particular cells. Nevertheless, theoretical models are useful, even in the absence of critical data, because they can indicate which data are needed, suggest previously uncontemplated experiments, or elicit modifications to routinely performed investigations and thus generate 'solid' new information.

In the area of low-intensity, low-frequency bioelectromagnetics, experiments that would contribute to the construction and verification of theoretical models might address:

The fundamental laws of electricity and magnetism are well understood, but they clearly allow a great variety of possible interactions with extremely complex, inhomogeneous, often anisotropic, and continuously varying living organisms. In the inanimate world, EMF have very different effects in electric motors, Xerox machines, radios, and computers. Only 50 years ago, understanding of the interaction of EMF with semiconductors was in its infancy, and new devices incorporating field effects are still being invented. There is no reason to believe that only one type of field coupling exists in the vastly complex, still poorly understood living systems. Different types of interaction are likely to be important at various field intensities in different organisms. Thus, several theoretical models may be appropriate for different intensities and in different biological environments. Valid quantitative models for the action of fields at the molecular level require quantitative understanding of biological processes, such as enzyme catalysis and biological signal processing. Figure 4.1 Equivalent circuit for an array of N membrane channels with conductive media on each side of the membrane (A discrete resistance value is associated with each channel (RG) and with each of the access resistances (RA and RB) near the channel mouths. All resistors in the circuit produce voltage noise, and these sources (VGi, VAi, and VBi) are completely independent and uncorrelated. When circuit analysis techniques with the proper methods are used for summing incoherent signals, the net noise voltage across an arbitrary channel (V1 in this figure) can be calculated. Note that the noise voltage of interest (V1) is that occurring across the channel, and not across the series combination of the channel and access resistances. The model assumes that any voltage gating mechanism is inside the channel or at the channel mouth. From Gailey (Gailey, 1996).

Figure 4.2 Normalized correlation coefficients for thermal electrical noise occurring across an ion channel as a function of the number of channels in the membrane (Electrical parameters used in this calculation apply to gap-junction channels with a channel resistance of 6.5 G  and an access resistance of 0.33 G .). The coherence or correlation between noise signals occurring in different channels decreases by a factor of 10 per decade with increasing number of channels. From Gailey (Gailey, 1996).

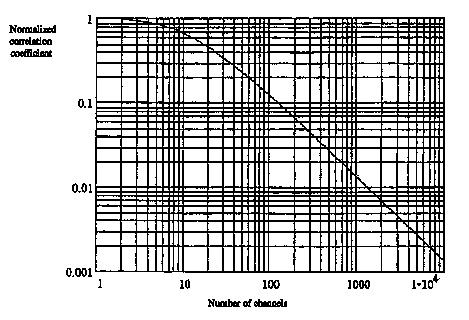
Figure 4.3. Improvement in signal-to-(thermal) voltage noise ratio due to lack of correlation between noise signals occurring in different open channels in the membrane (The x axis is the absolute value of the slope of the closing rate constant divided by the slope of the opening rate constant. The solid line was generated from equation 4.15 with equal opening and closing rate constants and assuming no effect of thermal voltage noise on the closing rate constants (  = 0, No-> oo.)). When the slight correlation between voltage noise in the open channels and the effect of the uncorrelated noise in these channels is included, the dashed line is obtained for a membrane with 50,000 open channels. From Gailey (Gailey, 1996).

Figure 4.4. Voltage noise spectra of a frog node of Ranvier at various membrane potentials. From Verveen and DeFelice (Verveen & DeFelice, 1974); reproduced by Barnes (Barnes, 1986).

Figure 4.5. Effect of magnetic fields on radical-pair energy levels (Electron spins in the three sub-levels of the triplet state: T+1 spins parallel in the direction of the magnetic field, T-1 spins parallel in the direction opposite to the magnetic field, T0 spins antiparallel but in phase in the field direction.). S, singlet state From Polk (Polk, 1992a).

Figure 4.6. Maximum change in escape probability and maximum relative change are shown as a function of cage retainment time for an increment of 5 µT to an external field of 50 µT (The recombination probability for electrons in a relative singlet state is taken as twice the escape probability and the internal field magnitudes and directions are selected from Monte Carlo procedures, as is the direction of the external field. The variation of escape probability with cage time of radicals with fields chosen so as to maximize the escape at a cage time of 10 ns, is also shown.) From Adair (Adair, 1997).

Table 4.46 Maximum numbers of turnovers of some enzymes

Enzyme
Turnover number (per second)
Carbonic anhydrase
600,000
3-Ketosteroid isomerase 
280,000
Acetylcholinesterase
25,000
Penicillinase
2,000
Lactate dehydrogenase
1,000
Chymotrypsin
100
DNA polymerase I
15
Tryptophan synthetase
2
Lysozyme
0.5
From Stryer (Stryer, 1989)

Table 4.47 Cells showing Ca++ oscillations

Cell
Stimulus
Period (s)
Rat myocyte Caffeine  0.3-3
Rat hepatocyte Vasopressin  18-240
Macrophage Cell spreading  19-69
Smooth muscle Phenylephrine or histamine  30-48
REF52 fibroblasts Gramicidin + vasopressin  35-100
Endothelial cells Histamine  40-125
B lymphocytes Antigen  50-75
Mouse oocyte Fertilization  600-1800
From Lauffenberger and Linderman (Lauffenburger & Linderman, 1993)

Table 4.48 Average endogenous fields due to heart activity induced field (Hz)

Induced field (Hz)
Tissue
0 - 40
F40 - 70
70 - 100
Brain 0.30  0.04 0.01
Cerebrospinal fluid 0.26 0.03 0.009 
Pineal gland 0.18  0.02 0.006
Pituitary gland 0.46  0.06 0.02
Eye humor 0.16  0.02 0.005
Lung 38.1  5.73 2.39
Heart 160  25.4 12.4
Liver 18.5  2.15 0.78
Stomach 33.8  3.75 2.06
Pancreas 15.1  1.64 0.61
Intestine 4.85  0.52 0.19
Kidney 4.42  0.54 0.18
Bladder 1.19  0.13 0.05
Prostate 0.91  0.10 0.04
Testis 0.35  0.04 0.01
From Hart and Gandhi (Hart & Gandhi, 1997)

Table 4.49 Experimental papers reporting resonance depending on the static magnetic fields (BDC)

Reference
Frequency
of
exposure
(Hz)
BAC
(T)
BDC
(T)
fR
(T)
Ion
Cells
organism
Exposure
duration
Effect
Notes
(Prato
et al.,
1996)		 60 299 peak 78+1 60 40Ca2+ Snails 15 min Attenuation of oploid-Included analgesia by approximately 20% BAC/and BDC variable 
(Yost &
Liburdy,
1992)		 16 42.1 23.4 16 45Ca2+ Mitogen-
activated
lymphocyte		 60 min Inhibits Ca Influx triggered by ConA No effect:
DC only
AC only 
(Tofani
et al.,
1995)		 32
50

32

 150 rms
75 rms

150 rms.
75, 150 rms

 42
 

0

 ND
 

ND

 40Ca2+ Human Lymphocytes 72 h Micronuclel formation frequency incresed 97 to 100%
6 subjects (marker of chromosomal damage)
No effect		 Genotoxic effect
 

Off resonance (no DC) 
(Blackman
et al.,
1994)		 45
25
45		 7.7-46.8
7.8-18.1
0.79-2.1		 36.6
20.3
2.0		 45
25		 Mg, V,
Mn
Li,H		 PC-12 Neuite
Outgrowth		 23 h Reduction of % cells with neuite outgrowth
No effect		 Subharmonics, BAC/BDC dependence
Off resonance (effect depends on NGF concentration) 
(Trillo
et al.,
1996)		 45

30

45

 0.29-4.11
rms
0.79-2.05
rms
0.79-2.05		 2.96

1.97

1.97

 45

30

 H+ PC-12 23 h Reduction of % cells with neurite outgrowth according to IPR, except near (Bac/Bdc) =0.85
No effect		 Effect at main resonance (n=1)
Off resonance 
(Jenrow
et al.,
1995)		 60
60		 10 peak
10 peak		 78.4
51.13		 60
60		 40Ca2+
K+		 Planaria 300 h Delay of cephalic regeneraton by 48 h
No effect		 Controls: BDC =18.2 T, or BAC=0
(Smith
et al.,
1987)		 60 20 peak 78.4,
39.2,
26.1,
153.3,
76.6,
51.1,
47.5,
9.5		 60 40Ca2+
K+
Mg2+		 Radish seeds 21 d Ca turning slowed germination, stimulates growth
K tuning speeded germination, inhibits growth.
Mg tuning did not affect germination, stimulates growth.		 Also AC unexposed controls
(Bowman
et al.,
1995)		 60 >0.3 38+
4.5
50.6
+
4.5		 29
39.5		 40Ca2+ Children 1-11 years Increase in childhood leukemia risk. Resonant DC fields B=fR / n for n = 2 & 3/2 are derived from Ca-efflux studies 
(Fitzsimmons
et al.,
1994)		 13.5-18 20 peak 20 16.3 45Ca2+ TE-85
Sa OS-2		 10 min.40 min. Increase of 45Ca uptake into bone cells 2 Hz, 50% band width
(Fitzsimmons
et al.,
1995)		 15.3 20 peak 20+
2		 15.3 40Ca2+ TE-85 10 min
optimum		 Increase of IGF-II release (human osteoscarcoma) DNA synt. incr. during 24 h post exposure
Maximum e = 1.6x10-5 V/m 
(Davies,
1996)		 60 14.4 78.3 Ca2+ Seeds (Replication of Smith et al.)
(Liboff
et al.,
1995)		 45, 25 7.7-46.8
7.8-18.1		 36.6
20.3		 Mg2+ PC-12
(Discussion of Blackman et al.)
(Blanchard
et al.,
1995) 		 45, 25 Several

(Response to above) 
(Blackman
et al.,
1996)		 45 12-35
perp.		 36.6
16.6		 Several PC-12
(Blackman
et al.,
1993a)		 50 < 10 44.7 PC-12
(Blackman
et al.,
1995)		 45 23.3 -
141.6		 36.6 Mg2+, Mn PC-12
(Blackman
et al.,
1998)		 45 23.8 36.6 ND PC-12
(Liboff
et al.,
1987)		 10-30 50-150 21 Ca2+ Human lymphocytes
(McLeod
et al.,
1987b)		 5-32 0-14.6 20.9 Ca2+ Diatoms
(Smith
et al.,
1987)		 16, 32, 48, 64 20.9 20.9 Ca2+ Diatoms
(Reese
et al.,
1991) 		 16 20.9 20.9  Ca2+ Diatoms 
(Prasad
et al.,
1991) 		 10-30 50-150 21 No Ca2+ Human lymphocytes
(McLeod
et al.,
1987a) 		 8-64 15 110.4
5,
20.9 		 Ca2+ , K+  Diatoms
(Smith
et al.,
1991b) 		 16, 80 14.14 12.7-
40.9 		 Ca2+,
Mg2+ 		 Chick femurs
ND, not determined