3 Internal Dosimetry
In chemical toxicology, the delivered dose of a xenobiotic is the concentration
of the substance at the cell or tissue of interest. When the toxicant is
a chemical, the dose can be measured using analytical devices. With EMF,
current knowledge indicates that the combination of the geomagnetic field,
AC magnetic fields, and electric fields and currents induced on or in the
body may affect biological processes. Because the exact mechanisms by which
these potential effects are produced have not been identified, however,
it is impossible to clearly define which aspects of EMF constitute the
dose. In studies of EMF, description of the relationships between external
EMF and the EMF and currents induced in the body is called 'dosimetry'.
The dosimetry of EMF can be estimated using the standard analytical techniques
of electromagnetics, although the significance of parameters other than
intensity must be considered. First, as EMF can be applied separately at
low frequencies (< 100 kHz), specifying whether the applied field is
electric or magnetic is essential. Second, because EMF are vectors, it
is essential to specify not only magnitudes but also field directions with
respect to the individual object (axial or transverse). For electric fields,
the shape of the exposed object greatly affects the induced currents, and
for magnetic fields the cross-sectional dimensions of the individual are
critical. In addition, for both electric and magnetic fields it must be
known whether the exposed object was electrically insulated or electrically
grounded.
The wave shape or frequency content of the applied signal also influences
delivered dose significantly. If the signal is purely sinusoidal and is
applied continuously, only the frequency and the duration of exposure need
to be specified; however, if pulsed fields are used, then specification
of wave shape, the rise time, decay time, duration of individual pulses,
and pulse repetition rate is essential. In general, the wave shapes of
applied magnetic and induced electric pulses are radically different.
Finally, a description of exposure to EMF should include measured values
of background fields, since these fields vary widely between laboratories.
These include the geomagnetic field, which is essentially static.
3.1 Electric field dosimetry for human exposure
Equation 2.1 in section 2 provides a rough approximation of the electric
fields inside and outside an individual subjected to an external electric
field. An electric field that is initially uniform becomes distorted in
the immediate vicinity of a person. Whether the individual is electrically
grounded or is standing on an insulating platform also will significantly
affect the field distribution (Table 3.1). Finally, for human exposure,
the interest is usually not in the average electric field within the body
but rather in the field and current density distribution within parts of
the body. The in homogeneity of electric properties (e.g. bone vs. muscle
conductivity) and variations in the cross-section of the limbs and trunk
determine the exact current density distribution. Extensive model calculations
and measurements have been made on 'phantoms' (saline body models) (Dawson
et al., 1997; Kaune & Forsythe, 1985). Thus, the maximum current
densities in a human standing on electrically conducting ground in a 10-kV/m,
60 Hz electric field are 0.03 A/m2 in the leg and 0.004 A/m2
in the neck.
Table 3.1. Typical average electric fields in bone marrow in numerical
dosimetric studies of uniform conditions of exposure to electric or magnetic
fields at 60 Hz
|
Vertical electric field (1 kV/m)
|
Organ-averaged electric field (mV/m)
|
| Grounded man |
3.0
|
| Insulated 14.4 mm above ground |
1.8
|
| Free space |
1.0
|
From Dawson et al. (1997)
Values are given for the tissues with the highest organ-averaged
electric fields for each exposure condition
Differences in shape, body size, and body orientation result in substantial
differences in induced electric field intensity with equal exposure to
external electric fields. Thus, rats in a cage must be exposed to a 30-kV/m,
vertical, 60 Hz electric field in order to obtain roughly the same current
densities within the rat body as inside a human standing upright in a 10-kV/m,
60 Hz field (Kaune & Phillips, 1980).
3.2 Low-frequency magnetic field dosimetry
3.2.1 Magnetic fields induced in the body by external magnetic fields
The ELF magnetic flux density, B(t), inside living tissues
is approximately equal to the external field. This relationship is a consequence
of two conditions. First, the magnetic permeability of tissue and cells
is approximately equal to that of free space. Second, the relatively low
electric conductivity (at most on the order of 1 S/m) of living matter,
in comparison with that of metallic structures (Å107 S/m),
guarantees that the magnitude of the secondary magnetic field produced
by the induced eddy currents is negligible (Polk, 1990). Therefore, the
applied magnetic field can be measured externally without need to correct
for the presence of an individual in the field.
3.2.2 Magnetic fields induced in the body by external magnetic fields
A time-varying magnetic field vector B also creates an electric
field E according to Faraday's law, such that
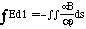Eq. 3.1
where d1 is a vector element of length and ds is a vector
element of area.
When a magnetic flux density B is applied parallel to the axis
of an infinitely long, electrically homogeneous, circular, cylindrical
body, equation 3.1 reduces to
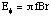Eq. 3.2
where E is the circumferentially directed electric field, f
is frequency, and r is the radial distance from the center of the
cylinder. This last relation is frequently employed in estimating induced
electric fields in animal bodies and cell cultures but will give only approximate
results because biological tissue is neither cylindrical nor electrically
homogeneous. Table 3.2 nevertheless shows that a 60 Hz, 1 µT magnetic
flux density B, orientated from the front to the back of an individual
will induce an electric field on the order of 100 V/m near the periphery
of the body. Detailed calculations are necessary to estimate induced field
intensities in organ systems (Dawson et al., 1997).
Table 3.2. Calculated average induced electric fields in selected tissues
in a human adult from a 1.0 µT, 60 Hz magnetic field orientated from
shoulders and assumed tissue conductivities
|
Organ
|
Tissue conductivity (S/m)
|
Induced electric field (µV/m)
|
| Brain |
0.1-0.17 |
11-12 |
| Cerebrospinal fluid |
1.5-2.0 |
2.8-5 |
| Lungs |
0.07-0.09 |
21-28 |
| Kidney |
0.27 |
14-24 |
| Prostate |
0.11-0.4 |
17-22 |
From Dawson et al. (1997)
Depending on the biological interaction mechanism, either the internal
magnetic field or the induced electric field is the appropriate applied
dose.
3.3 Scaling between different organisms, assuming that an observed effect
is due to induced electric fields
Equations 3.1 and 3.2 indicate that the magnetic flux density B
would have to be varied in inverse proportion to the radius r (in
a plane perpendicular to the direction of B) if the same induced
electric field is to be obtained in different preparations or organisms.
Thus, assuming that a particular physiological system is similar in mice
and humans, a 10 µT, horizontal, 60 Hz magnetic field in a mouse
of 2.5-cm diameter and a 1 µT, vertical 60 Hz magnetic field in a
human of 25-cm mean body diameter would produce similar effects.
Because the electric properties of biological substances can change
substantially over a scale of nanometers (for example when a membrane is
present), predictions of the electric field at every point in a tissue
are therefore accurate on a micro-scale only when regions of tissues are
correctly represented.
Electric fields inside the human or animal body induced by time-varying
ELF magnetic fields will not necessarily produce the same biological effects
as internal electric fields due to externally applied magnetic fields.
Scaling between different organisms or from in-vitro to in-vivo conditions
will differ widely for external electric and magnetic fields, even if the
magnetic field exerts its physiological effect only through induced electric
fields or current densities. In the absence of detailed numerical micro-scale
models, equation 3.2 must be used for first-order scaling.
3.4 Considerations for in vitro dosimetry
Several experiments (Blackman et al., 1994; Liboff et al.,
1987) have shown that certain biological effects depend on synergism between
static and time-varying magnetic fields, suggesting that both magnitude
and relative field direction are important. Inside a steel-frame building
or a laboratory incubator, the 'static' magnetic field may differ substantially
in both magnitude and direction from the field in free space and may also
vary from point to point. Specifying the characteristics of the background
field at the exposure location is therefore essential when biological effects
of weak (microtesla) magnetic fields are investigated. Similar considerations
are not needed for electric fields because they are substantially lower
in saline than in air.
3.4.1 Electric field dosimetry
Culture media generally have an electric conductivity on the order of 1
S/m, similar to that of fluid-saturated living tissue. A material is considered
to be an electric conductor, as opposed to an insulator or dielectric,
if the ratio of conduction current density, , to displacement current density,
t), is much greater than 1, where is the electric conductivity,
E is the electric field, and is the dielectric permittivity. For
a field that varies sinusoidally in time at a frequency of , this relationship
is:
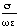>> 1 Eq. 3.3
The dielectric permittivity is given by 10, where 0
is the permittivity of free space, which is equal to 8.84 x 10-12
F/m, and 1 is the relative dielectric constant. Below 100 Hz,
the 1 of living tissue can be as large as 106; nevertheless,
equation 3.3 still gives a value of 180 at 100 Hz with = 1 S/m and r
= 106. Thus, at ELF, culture media can be considered to be electrically
conducting fluids. Electric fields are therefore most easily introduced
into cell cultures by contact and by measuring the series current, I.
If the electrodes are large enough and their shape is relatively simple,
or if the field is calculated at a point in the field at a distance that
is relatively far in comparison with the electrode size, then the electric
current density, J, is given by I/A, where A is the
cross-sectional area of rectangular electrodes or of rectangular vessels.
The electric field can then be calculated from J = if the conductivity
is measured.
All such calculations are based on the assumption that the culture medium
of cells and tissues is electrically homogeneous. This approximation is
reasonable for freely floating cells at relatively low density. If cells
are plated at the bottom of a culture vessel and become confluent, or nearly
so, the culture fluid and cell system must be considered a two-layer medium,
in which the bottom (cell) layer may have vastly different (and at ELF
usually lower) electric conductivity than the fluid. Current density and
field evaluation then require more complex calculations.
Electrodes must be introduced cautiously into biological fluids in order
to avoid chemical reactions at the electrode surfaces and consequent contamination
of the fluid. The most successful method is use of agar bridges. Another
method for introducing an electric field into a culture medium is capacitive
coupling (Polk, 1995).
3.4.2 Magnetic field dosimetry
A key question in exposure to magnetic fields is the magnitude of the induced
electric field. Here, the orientation of a culture dish or any other object
within the magnetic field will have major consequences because only the
component of the magnetic field that is perpendicular to a surface contributes
to the induced electric field in the plane of that surface; different orientations
of the magnetic field to the culture dish result in significantly different
induced electric field magnitudes and distributions. In the immediate vicinity
of a high-voltage transmission line, the electric field induced in a human
by the electric field of the line will generally be larger than the electric
field induced by the line's magnetic field. Conversely, inside a home or
even near a secondary distribution line, the electric field induced inside
the body will usually be due to the external time-varying magnetic field
(King, 1998; King & Wu, 1995).
3.5 Summary
The occurrence of static and dynamic EMF in the environment will result
in the induction of magnetic and electric fields in the body. Because of
the low permeability of living tissues, both static and dynamic magnetic
fields within the body will be similar to the magnetic fields outside the
body. Conversely, the induction of electric fields in the body due to either
time-varying electric or magnetic fields requires careful numerical calculations
which incorporate size, shape, and organ conductivity. Peak induced electric
fields in the human body due to exposure to a 60 Hz, 1 µT magnetic
field can exceed 0.1 mV/m. Similar computational techniques can be used
to determine induced fields in laboratory experiments.